[最も欲しかった] 直線 の 公式 257523-直線の公式 3次元

電線(直線)は、デバイスに電気を供給するために使用されます。 このケーブルを電力網で使用して、 Generatorを Electrical Outletに接続し、近くの電気機器に電力を供給することができます。 電線(直線)は木製の建造物として扱われ、手、石の武器、非爆発的な遠距離攻撃によって損傷することは数直線上における外分点の公式に2点\(A,B\)の値と、外分する比\(mn=21\)を代入します。 外分点を求めるときは\(n\)を掛けることに注意しましょう。 \(\displaystyle \frac{namb}{mn}=\frac{1 \cdot 4 2 \cdot 7}{21}=10\)2点を通る直線の方程式 切片を用いた直線の方程式 2直線の交点の座標 3点の座標で囲まれる三角形の面積 座標点で囲まれる多角形の面積 座標の回転 座標軸の回転 直交座標から極座標へ変換 極座標から直交座標へ変換

図形と方程式 点と直線 公式 大学受験の王道

直線の公式 3次元

直線の公式 3次元-直線の方程式は であるので、外積は、 これらのベクトルの外積を求めればよい のいずれにも垂直なベクトルを求める 直線の方程式は と解釈する。 分母にがあるが、これは, 2 3 3 8 1 0 =− − − = − y x z1)直線が y 軸に平行でないとき 傾きを m ， y 切片を n とすると，直線の方程式は y = mx n ⇔ mx − y n = 0 2)直線が y 軸に平行なとき x 軸との交点の座標を (p, 0) とすると，直線の方程式は x = p ⇔ x − p = 0 以上1)，2)のいずれの場合でも，直線の方程式は x

関数07 放物線と直線の公式 Youtube

直線の方程式(2点を通る)の公式を証明！平行や垂直な場合の こんにちは、ウチダショウマです。 今日は、中学生でも習う 「直線の方程式」 について、数学Ⅱの図形と方程式ではどんな知識を得られるのか、スッキリ解説しようと思います。(4) y £ mx b 的圖形為直線 L 及直線 L 的下側半平面。 2 設直線 L ： ax by c = 0 ，其中 a > 0 ，則 (1) ax by c > 0 的圖形為直線 L 的右側半平面。 (2) ax by c ³ 0 的圖形為直線 L 及直線 L 的右側半平面。 (3) ax by c < 0 的圖形為直線 L 的左側半平面。 (4) ax by c 直線という図形を式で表す 前回までは座標平面で 「点」 を扱ってきましたが、ここからは 「直線」 について考えてみましょう。 なぜ直線を扱うかというと、 三角形・四角形などの図形は直線（線分）でできています よね。 ですから直線を扱えることはつまり、座標平面でそのような

直線の場合は、どの範囲を使っても傾きは同じになります。 3．傾きの計算2 それでは、次のy=2のグラフの傾きはいくつになるでしょうか？ う～ん、見る限り直線は傾いているようには見えないですね。 一応、傾きを求める公式に入れて計算してみましょう。回帰直線 テストの得点 (Y)を勉強時間 (X)で説明するにあたって、ここでは、一次関数 y = a bx を利用する テス 回帰直線 この一次関数から得られる直線 切片 (a) 説明変数が最小の場合のYの値 傾き (b) 回帰直線の傾き 切片 (a)と傾き (b)の値を動かすこと 直線の式 1 1 ： 傾きが a a であり， y y 切片が b b の直線の方程式は， y = ax b y = a x b 傾きと 1 1 点

どの問題提示のときに3つの公式のどれを使って解を求めるかがわかりません。 解説 まず公式の意味を確認していきましょう。 ①v＝v 0 ＋atについて これは，初速度v 0 ，加速度aで等加速度直線運動している物体が，時刻tにどのような速度vになって 公式2より求める直線の方程式は， (ba) (y2)= (32) (xa) (b− a)(y− 2)= (3− 2)(x−a)2点を通る直線の方程式 2つの点(x₁、y₁)と(x₂，y₂)を通る直線の方程式は、次の公式で求めます。 で直線の傾きを求めていることに注目です。 練習問題 点(3、2)と(5，4)を通る直線の方程式を求めなさい。 先ほどの公式に値を

２点 直線の方程式

勉強しよう数学 垂直な直線の方程式

 中学数学では、 に 座標と 座標を代入し、 を計算することにより直線の方程式を求めていたかと思います。 しかし、高校数学ではいちいちそのような計算を行わず、直線の方程式は公式を用いて求めることができるようになります。 簡単公式2直線の交点の座標を3秒で計算できる求め方 2直線の交点の公式をおしえてほしい。。 こんにちは！この記事をかいているKenだよ。アップルパイは1日2本だね。 よく最近、 2直線の交点の座標をもとめる公式 ってあるの？？ ってきかれるんだ点と直線の距離を求める公式を使ってみよう！ 点と直線の距離を求める練習問題 点と直線の距離を求める公式まとめ！ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる！ こちらの関連記事はいかがでしょうか？

3分でわかる 点と直線の距離の公式の証明 使い方のコツを分かりやすく 合格サプリ

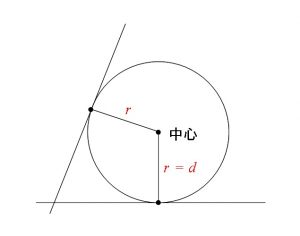
円に接する直線 接線の方程式 の求め方３パターン

直線の方程式の標準形 において，方向ベクトル のいずれかの成分が0であるときは，その分数の分子も0になるものと解釈する． 例1 点 を通り，方向ベクトル に平行な直線の方程式 の標準形を上記の公式を用いて形式的に書けば (1) となるが，この式の第2辺は「分母が0になっているから 直線の方程式（傾き・切片） 中学で学習した 直線の方程式 は、 傾き と 切片 を用いて表された式です。 グラフは以下の通りです。 比例の関係を表すグラフは 原点 を通る直線となります。 それを y軸方向へ切片のぶんだけ平行移動した ものが、直線の方程式が表すグラフです。よって求める直線は(0,0)と(10, 4)の2点を通る直線である。 よって y= 2 5 x (2) 点Bを通って AOBの面積を二等分する直線は、Bの対辺であるAOの中点を通る。 AOの中点は(4,4)なので、求める直線は(4,4)と(12,0)を通る。 よって y=− 1 2 x6 (3)

原点と直線の距離の公式の証明 図形と計量

図形と方程式 点と直線 公式 大学受験の王道

 点と直線の距離の公式は見た目は複雑ですが、 図形と方程式の問題を解く上で欠かせない公式 です。 13年の大阪大学の入試で点と直線の距離の公式の証明がそのまま問題になる など、きちんと証明できるかどうかも問われています。直線補間法 2点間を補間する方法として、直線補間が一番容易である。 始点 (xs,ys)、終点 (xe,ye)とするとき、任意のxに対応する2点を結ぶ直線上のy値は次式となる。 y = ys ( x xs ) ( ye ys )/ ( xe xs ) ・・・ (1) Excelを用いた直線補間 図2のように、始点と b ≠ 0 なら，直線 ℓ a x b y c = 0 の傾きは − a b になります．つまり， a と b の比が直線 ℓ の向きを決めるということになります． こう考えると，係数比 a b を考えれば 平行条件も 垂直条件も得られることになります． 実際，2直線 ℓ 1 a 1 x b 1 y

高校数 図形と方程式 ２直線の交点を通る直線 理由 確認 オンライン無料塾 ターンナップ Youtube

点と直線の距離の公式で分子の絶対値を外したら にならないんですか Clearnote

または －1）） である場合は，2直線が一致せずに平行となるので，交角はありません． 19 2直線の中央線（交角の2等分線） 直線 と直線 の中央線，すなわち2直線 l1,l2 からの等距 離線 LAx By C 0 の係数 A,B,C は次のように求めます．ただし，直線 L① v ＝ v0 ＋ at について これは，初速度 v0 ，加速度 a で等加速度直線運動している物体が，時刻 t にどのような速度 v になっているのかを表しています。 円と直線の位置関係 円と直線の位置関係は 異なる2点で交わる 1点で接する 共有点を持たない のいずれか。 円と直線の関係の判定方法 円の中心から直線までの距離と円の半径を比較して判定する。 （点と直線の

点と直線の距離を求める公式とその証明 数学ii By ふぇるまー マナペディア

中1数学 直線の式の求め方 練習編1 映像授業のtry It トライイット

（公式Ⅱの解説） 2点 (a, b), (c, d) を通る直線の方程式をいきなり考えると，点が2つもあってポイントが絞りきれないので，1点 (a, b) を優先的に考える． すなわち，2つ目の点 (c, d) は傾きを求めるための材料だけに使う． このとき，2点 (a, b), (c, d) を通る直線の傾きは通る2点が与えられた直線の方程式 異なる2点 ( x 1, y 1), ( x 2, y 2) を通る直線の方程式は y − y 1 = y 2 − y 1 x 2 − x 1 ( x − x 1) である．ただし， x 1 ≠ x 2 とする． x 1 = x 2 のとき，直線の方程式は(4)直線的關係已知直線Laxbyc=0 a直線L1平行直線L↔mL 1 =mL↔設直線L1axbyh=0 b直線L2垂直直線L↔mL 2 ∗mL=−1↔設直線L2bxayk=0 (5)直角坐標平面上之公式 a內分點公式 設點A(x1,y1),點B(x2,y2),若P(x,y)在AB̅̅̅̅上,且A̅̅̅P̅P̅̅̅B̅=mn, 則點P 為AB̅̅̅̅之內分點,且P

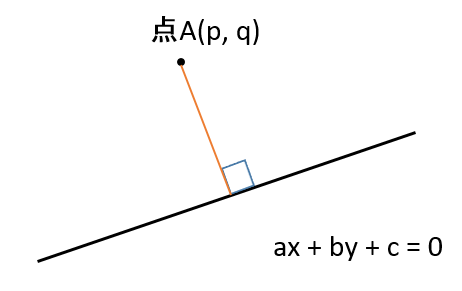
中学生でもわかる 点と直線の距離の公式の証明 偏差値40プログラマー

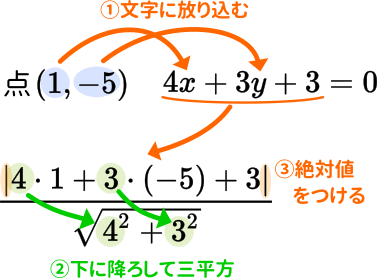
数 図形と方程式 点と直線の距離の公式をビジュアルで覚える Mm参考書

点と直線の距離を求める公式 まず「点と直線の距離」ときいて、何を思い浮かべますか？ 図のような点Pと直線lの距離を求める方法についてみていきましょう。 図のように、直線l："ax＋by＋c＝0"上に} ` ƕ @ q _ Ԃ̋ ̂Ƃ a f ɕ _ @ ̂Ƃ a f ɕ _ ́a j ̂Ƃ o _ b ̕ x Ła _ ʂ f q _ ʂ f j ꂪ o ̂Ƃ a ͍ w ƕ s Ȓ

放物線上の2点を通る直線の式 から 切り取られる線分の長さ へ うしブログ

3

數學公式 直線方程式的求法 已知線上兩點 博志bojhih 國中資優數學理化 痞客邦

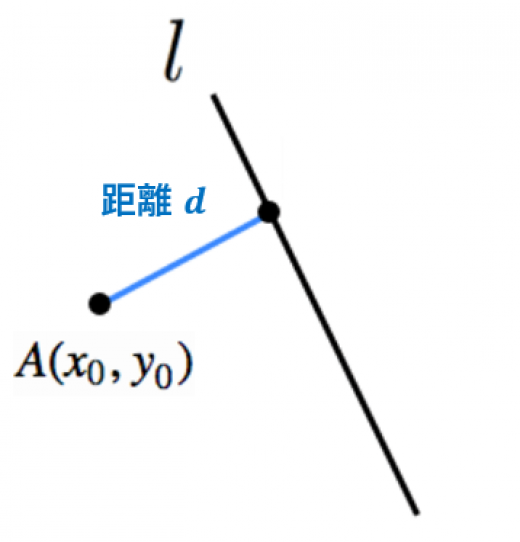
点と直線の距離公式の３通りの証明 高校数学の美しい物語

点と直線の距離の公式とは 3次元やベクトルを用いた証明も解説 阪大入試問題 遊ぶ数学

点と直線の距離公式をベクトルを使って導く すうがくブログ 式変形ch

図形と方程式 直線の方程式について 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開

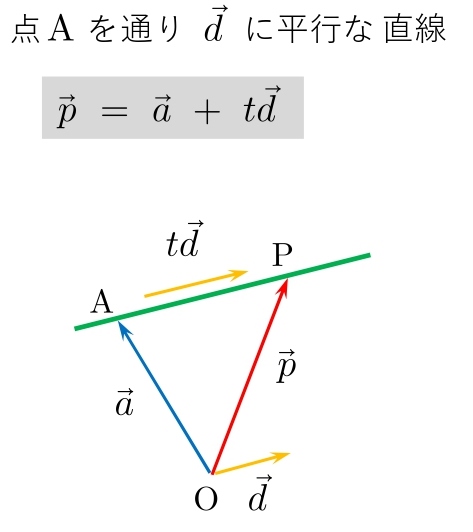
高校数学ｂ ベクトル方程式 公式一覧 直線 円 存在範囲 学校よりわかりやすいサイト

点と直線の距離

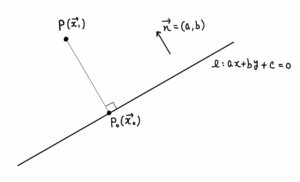
点と直線の距離公式をベクトルを使って導く すうがくブログ 式変形ch

基本 垂直な直線の方程式 なかけんの数学ノート

山と数学 そして英語 高校数 図形と方程式 直線の方程式の求め方 その４

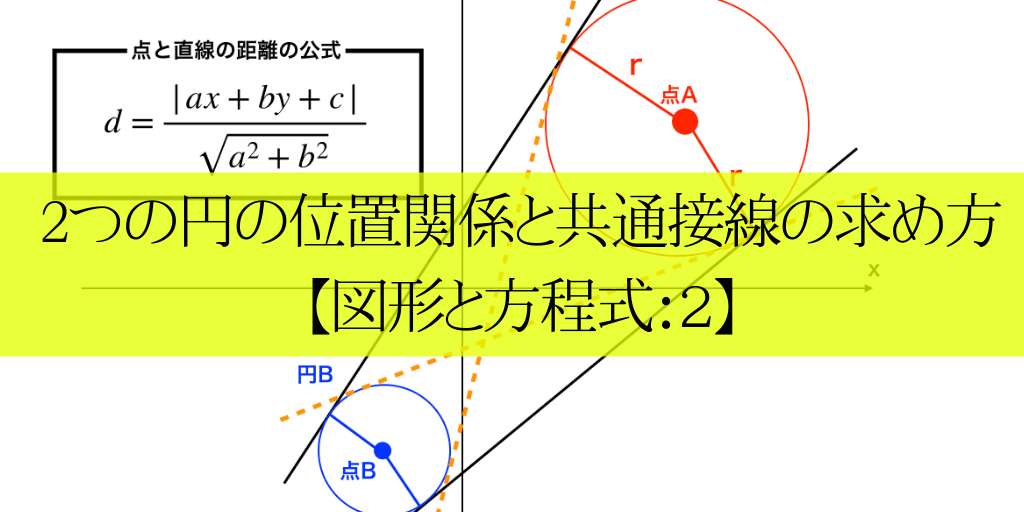
2つの円の位置関係と共通接線の求め方 図形と方程式 2

数学 図形と方程式 点と直線の距離 の公式の導出 オンライン無料塾 ターンナップ

点と直線の距離の公式とその使い方 高校数学の知識庫

高校数学 直線の傾きによる2点間の距離の公式 放物線の弦の長さ 受験の月

数学 平行な直線と垂直な直線の求め方とコツ 教科書より詳しい高校数学

山と数学 そして英語 高校数 図形と方程式 直線の方程式の求め方 その２ 垂直に交わる直線

高校数学 点と直線の距離の公式 映像授業のtry It トライイット

數學公式 直線方程式的求法 已知線上兩點 博志bojhih 國中資優數學理化 痞客邦

点と直線の距離 東大合格コム

直線の方程式 数学ii フリー教材開発コミュニティ Ftext

直線の式の求め方 思考力を鍛える数学

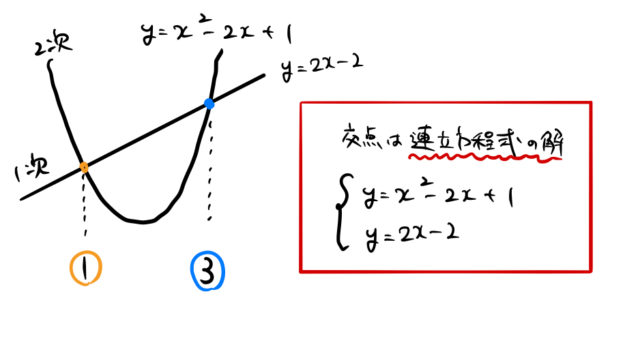
高校数学 面積を求める 1 6公式 1 12公式 1 30公式などパターンまとめ ばたぱら

点と直線の距離とは 公式や証明 計算問題 受験辞典

直線と直線の距離の公式と最近点 理数アラカルト

中３数学 ２次関数総合 頂点を通らない三角形の２等分線

高校数学 直線の方程式の求め方 １点 傾き オンライン無料塾 ターンナップ Youtube

ベクトル方程式とは 図形別の公式 直線 円 や問題の解き方 受験辞典

関数07 放物線と直線の公式 Youtube

一次関数 2点を通る直線の式の求め方をイチから解説 Youtube

高校数学 点と直線の距離の公式とその証明 受験の月

中1数学 直線の式の求め方 練習編1 映像授業のtry It トライイット

点と直線の距離の公式 正射影ベクトルを用いた証明法 ぷっちょのput Your Hands Up

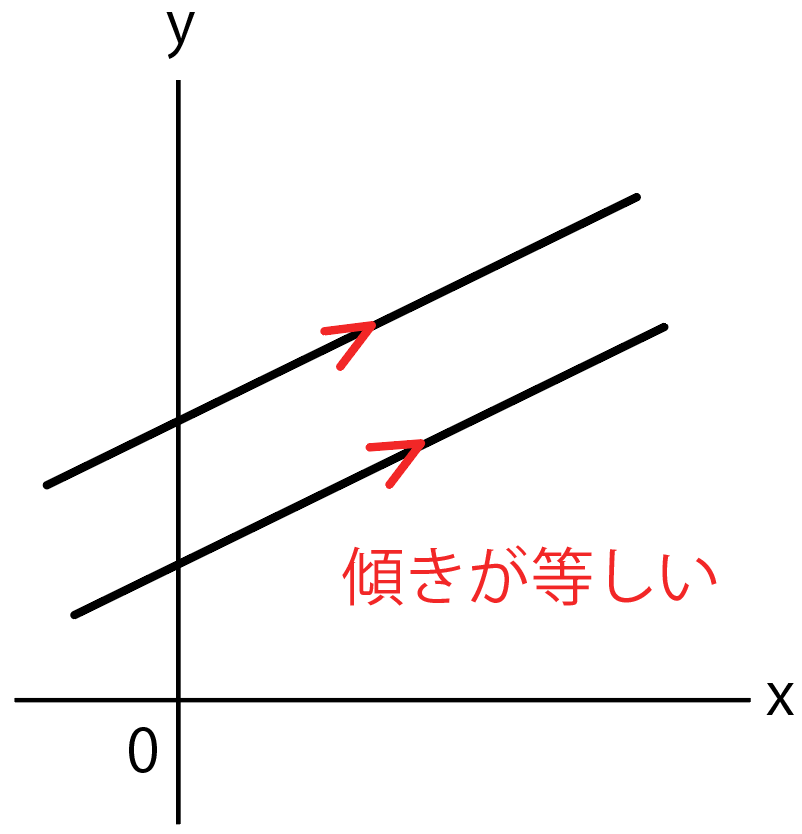
一次関数 テストに出やすい 平行な直線の式の求め方 Qikeru 学びを楽しくわかりやすく

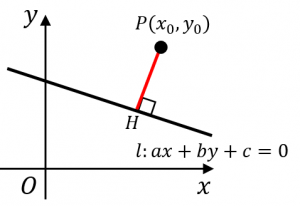
点と直線の距離の公式の意味と中学数学範囲での証明 具体例で学ぶ数学

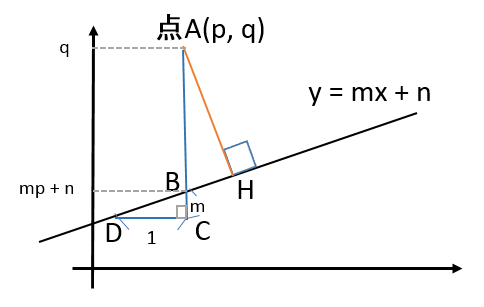
中学生でもわかる 点と直線の距離の公式の証明 偏差値40プログラマー

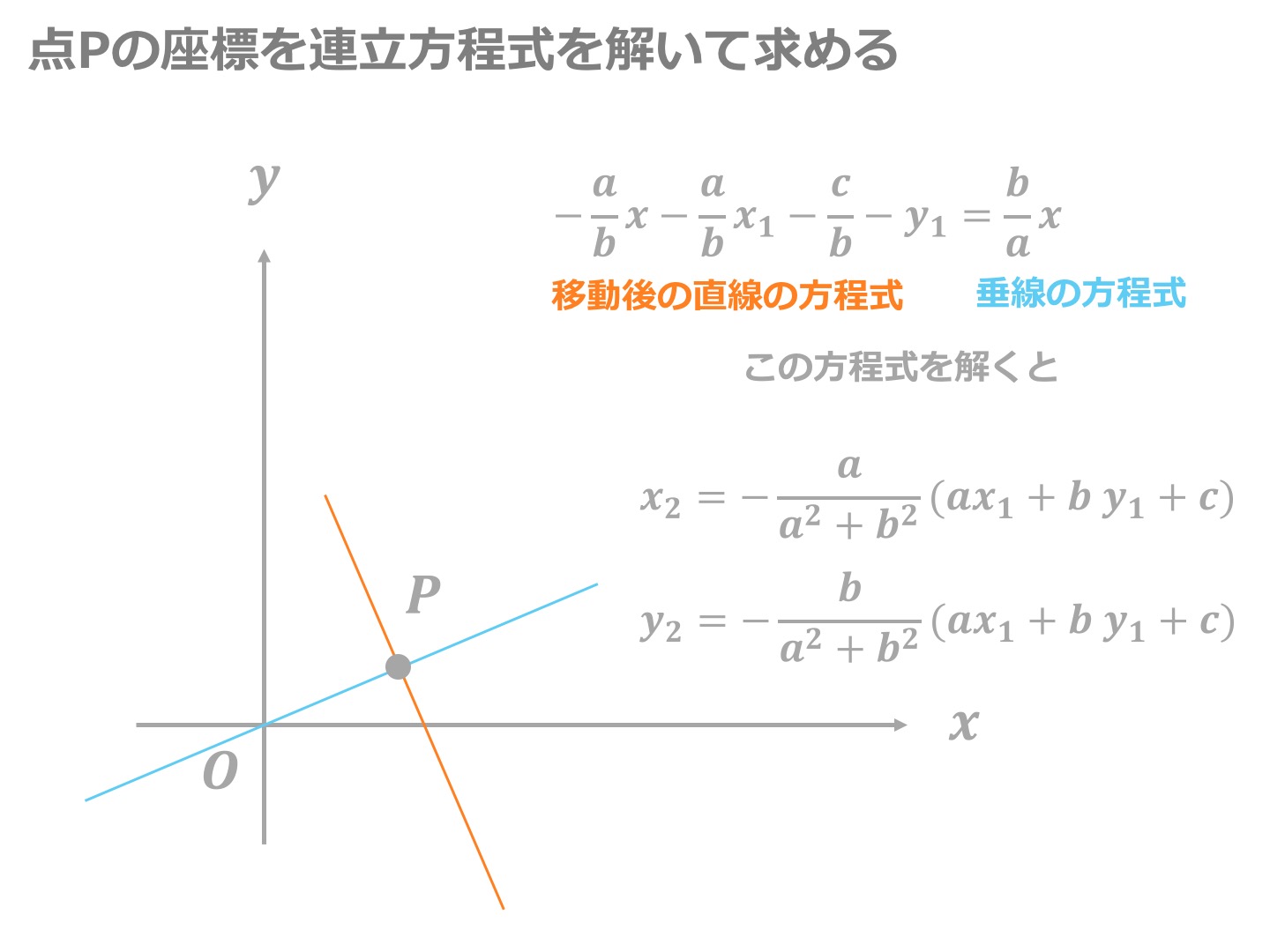
3分でわかる 点と直線の距離の公式の証明 使い方のコツを分かりやすく 合格サプリ

点と直線の距離を求める公式とその証明 数学ii By ふぇるまー マナペディア

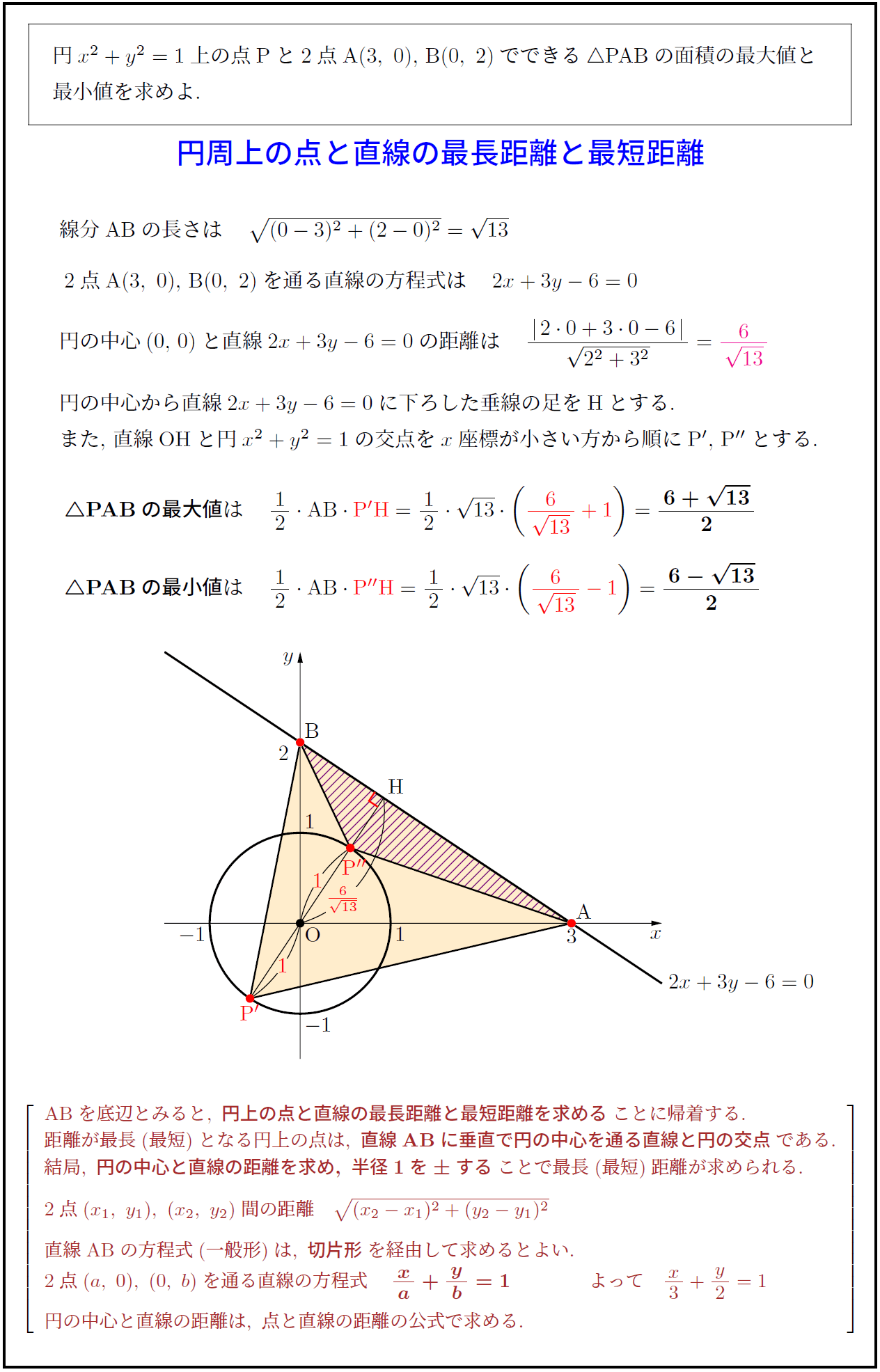
高校数学 円周上の点と直線の最長距離と最短距離 受験の月

高校数学 直線の方程式 練習編 映像授業のtry It トライイット

高校数学 円と直線の位置関係 受験の月

微分を使った接線に垂直な法線の方程式の求め方と公式

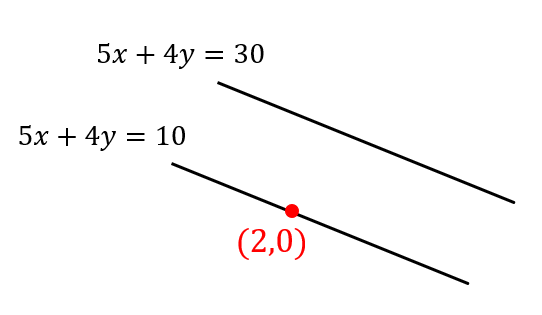
直線と直線の距離 平行な2直線の距離を求める方法を解説 サクッと解けちゃうぞ 数スタ

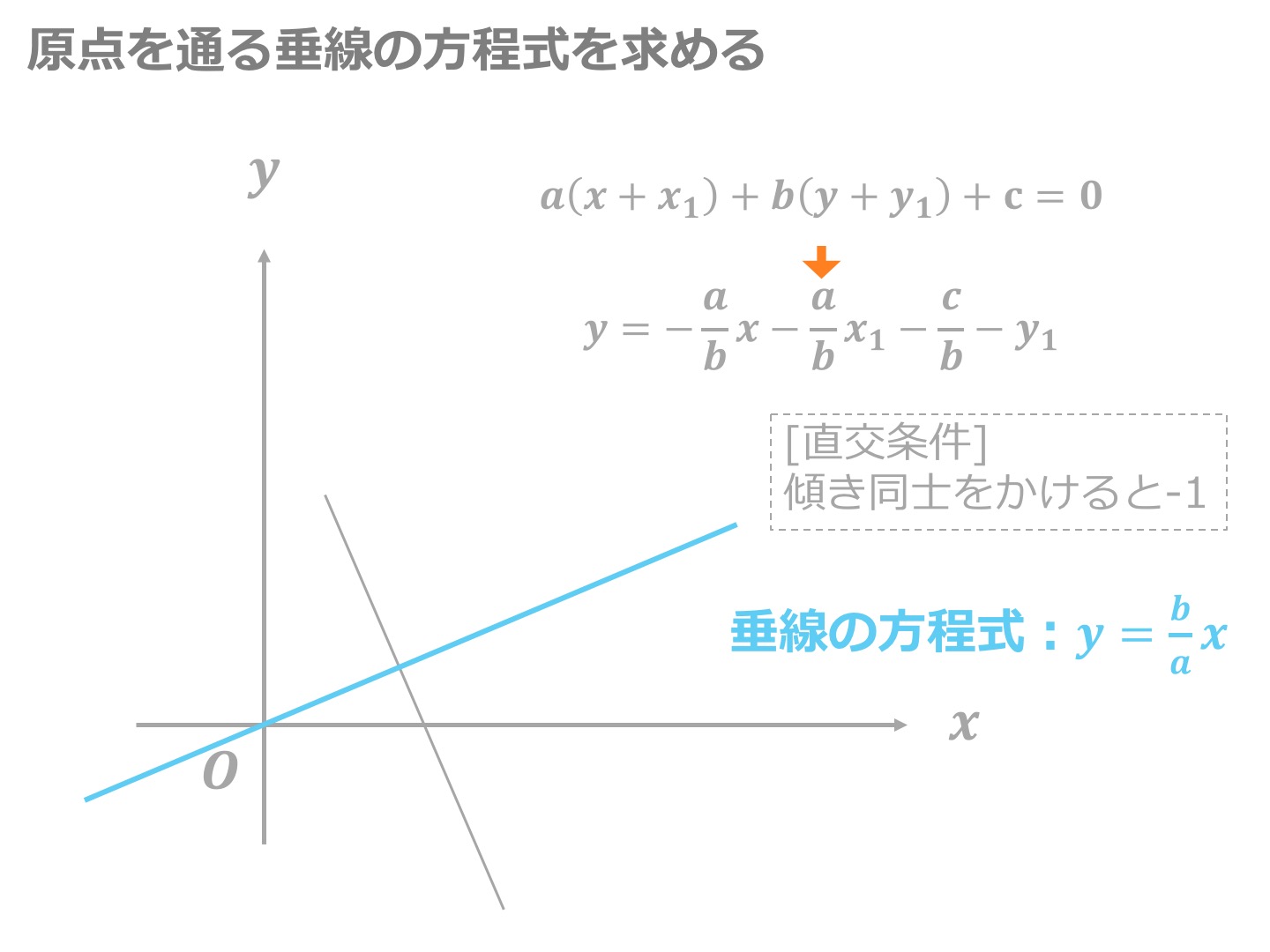
3分でわかる 点と直線の距離の公式の証明 使い方のコツを分かりやすく 合格サプリ

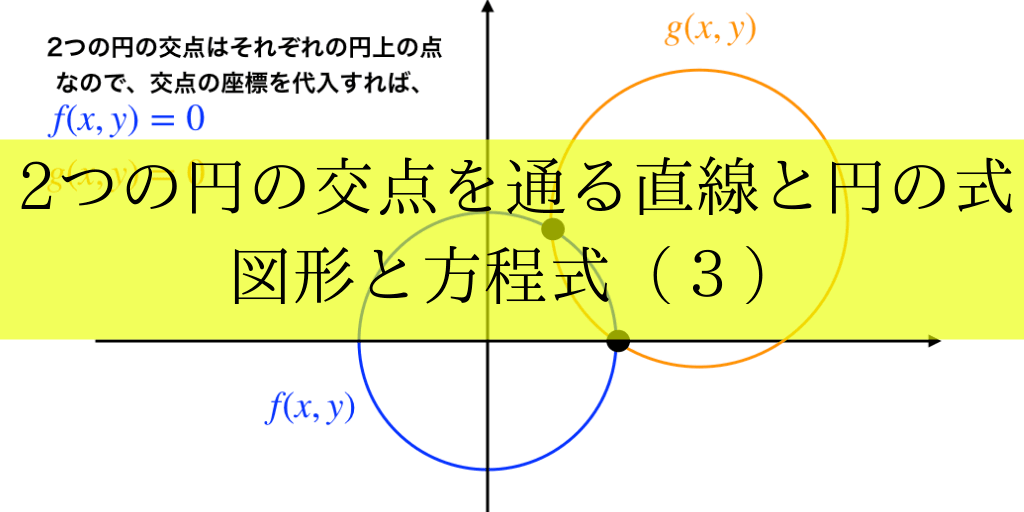
円どうしの交点を通る直線 曲線の式の解説とその理由 束

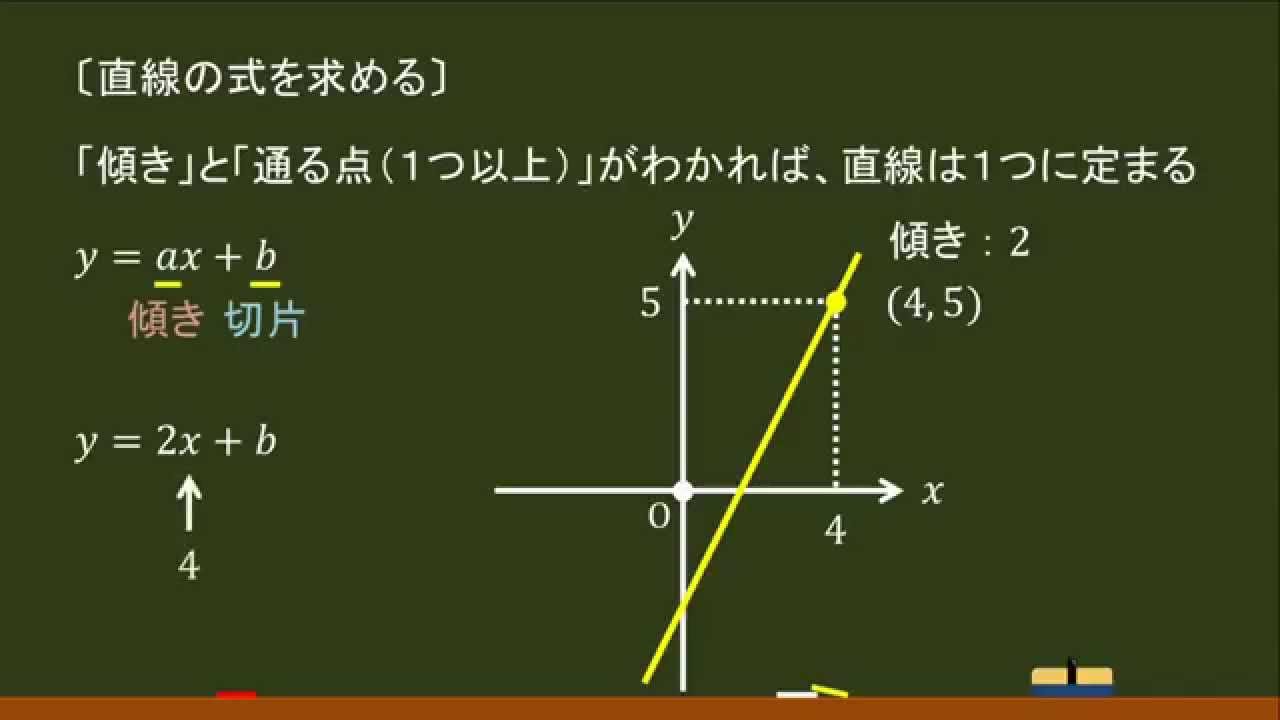
中２数学 １次関数 直線の式を求める 傾きと通る１点から オンライン無料塾 ターンナップ Youtube

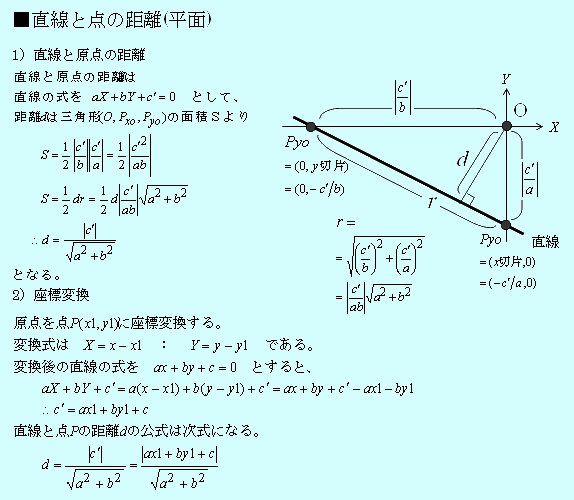
直線と点との距離 高精度計算サイト

中３ ２直線の平行条件 垂直条件 鉄緑会数学講師のひとりごと

数学用語解説 数 図形と方程式 軌跡と領域

直線と放物線の面積算出の1 6公式 Thoth Children

最速 放物線上の2点を通る直線の式を簡単に求める方法 大学入試数学の考え方と解法

直線と直線の距離の公式と最近点 理数アラカルト

Q Tbn And9gctcj6w5hlvl3fax2o1sigai Pbco1qvgoabehcatlhvalcryvqe Usqp Cau

公式証明道場1 点と直線の距離の公式 数 Aで学びたい高校のnote塾 Note

図形と方程式は2時間で解けるようになる 外資系コンサルタントが主夫になったら

等加速度直線運動の３公式の使い方がわかりません 理科 苦手解決q A 進研ゼミ高校講座

直線の方程式の公式を教えて下さい 平行verも教えていただけると幸いです Clearnote

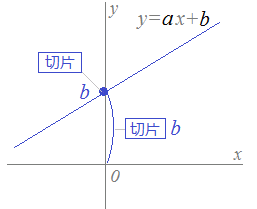
1次関数 グラフ 直線の方程式

3つの証明 点と直線の距離の公式 D Ax By C A B 数学ii Youtube

直線の方程式 2点を通る の公式を証明 平行や垂直な場合の傾きの求め方も解説 遊ぶ数学

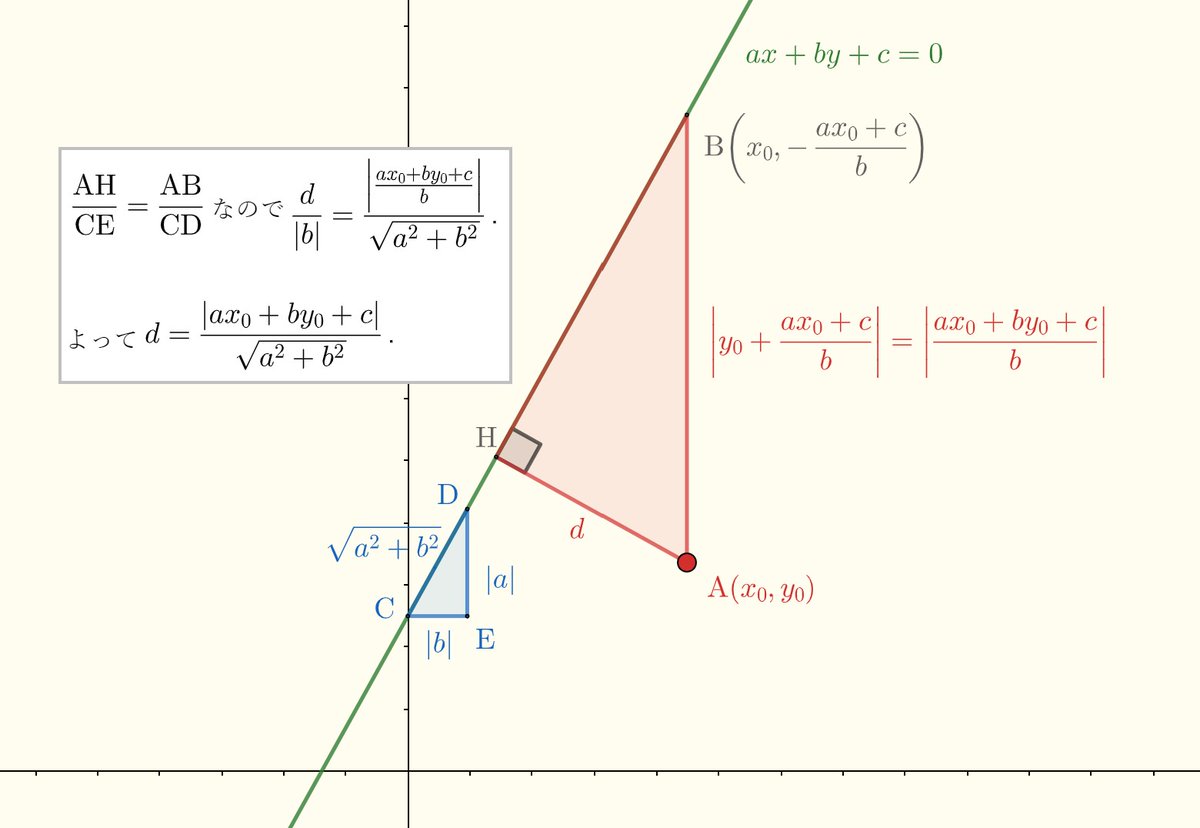
コロちゃんぬ على تويتر 点と直線の距離の公式 三角形の相似で証明できるの知らんかった

数学 図形と方程式 点と直線の距離 の公式の導出 オンライン無料塾 ターンナップ

等速直線運動 高校物理をあきらめる前に 高校物理をあきらめる前に

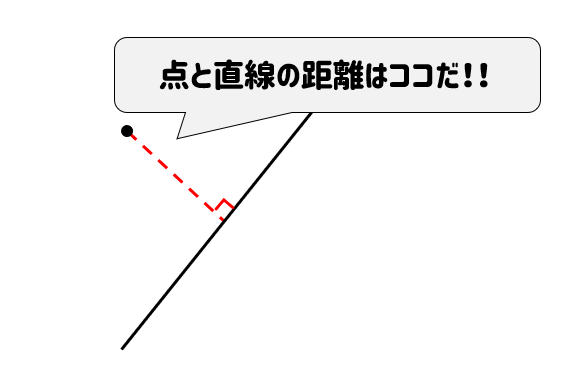
点と直線の距離 公式の覚え方と使い方をイチから解説するぞ 数スタ

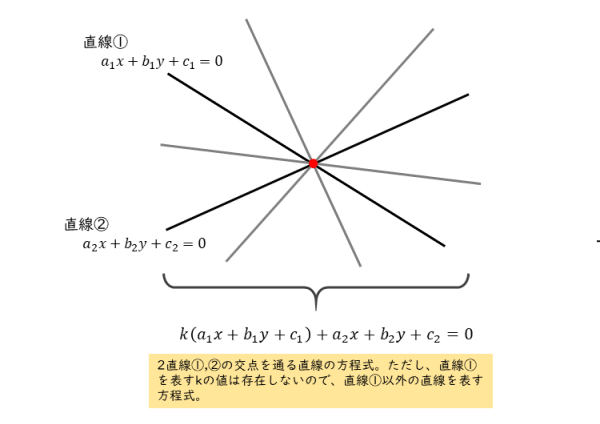
図形と方程式 ２直線の交点を通る直線について 日々是鍛錬 ひびこれたんれん

通る1点と傾きが与えられた直線の方程式 数学ii フリー教材開発コミュニティ Ftext

点と直線の距離とその証明 おいしい数学

数学公式 点と直線の距離の公式 は2次試験の前に 証明を確認しておきたい 学習村の 国公立へ行こう

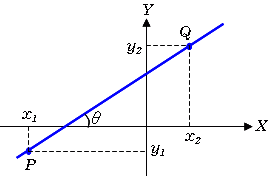
２点を通る直線の方程式 高精度計算サイト

点と直線の距離の公式の覚え方 証明の方法や練習問題も解説 高校生向け受験応援メディア 受験のミカタ

点と直線の距離の公式

点と直線の距離 画像処理ソリューション

中学 高校数学公式bot 数 図形と方程式 1 点 X1 Y1 を通り傾きmの直線の方程式 2 2点 X1 Y1 X2 Y2 を通る直線の方程式 3 Y軸に平行な直線の方程式 4 X切片がa Y切片がbの直線の方程式 T Co 9huvsyf7go

2直線の関係 平行と垂直 高校数学の知識庫

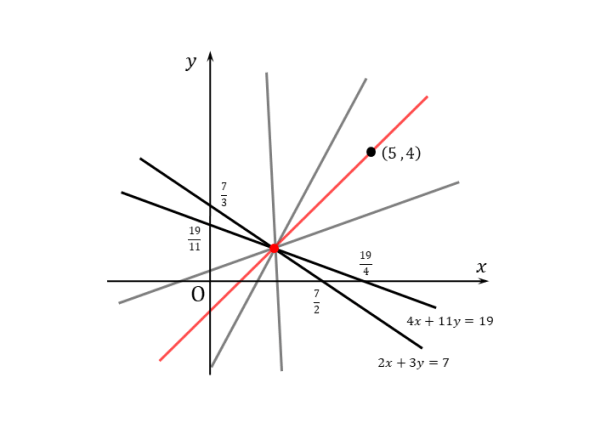
図形と方程式 ２直線の交点を通る直線について 日々是鍛錬 ひびこれたんれん

点と直線の距離公式の３通りの証明 高校数学の美しい物語

点と直線の距離の公式を法線ベクトルから求める ラディカル高校数学

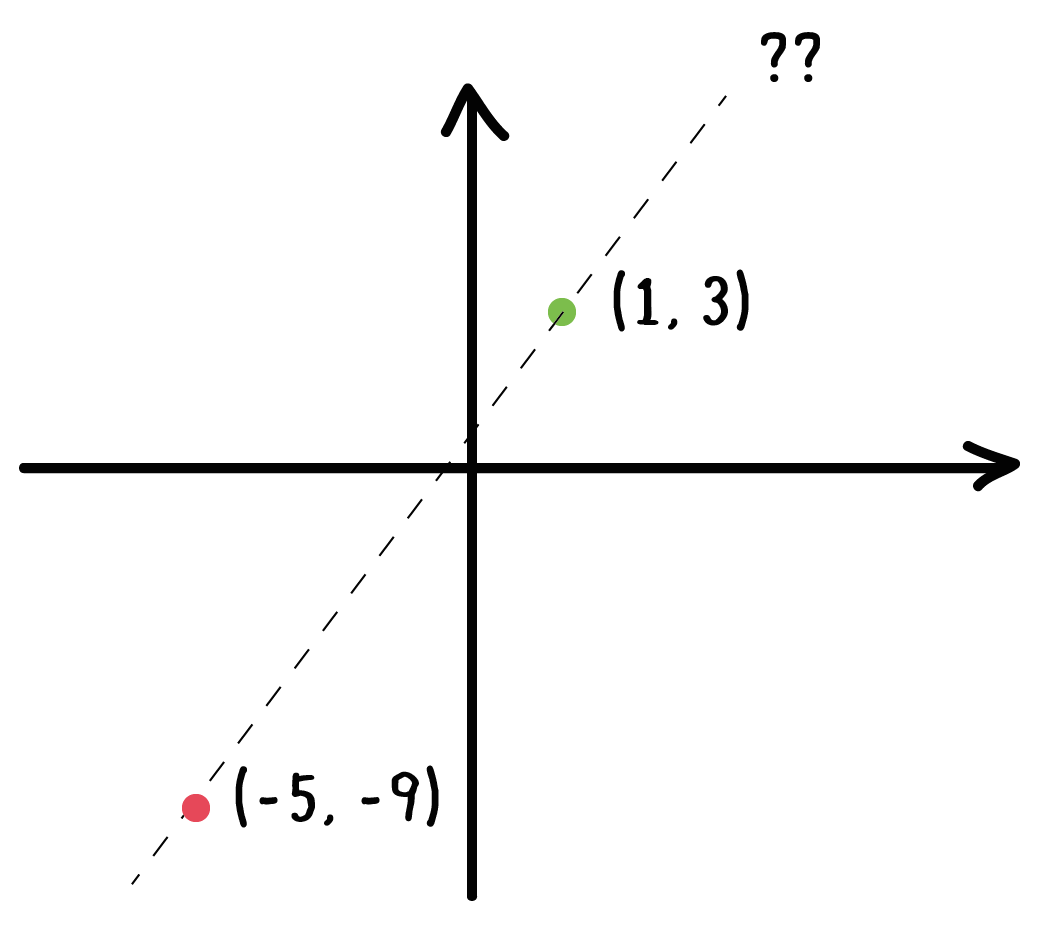
1次関数 2点を通る直線の式の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

直線と点との距離を求める公式 ２０１３年大阪大学文系前期入試問題から 身勝手な主張

点と直線の距離とその証明 おいしい数学

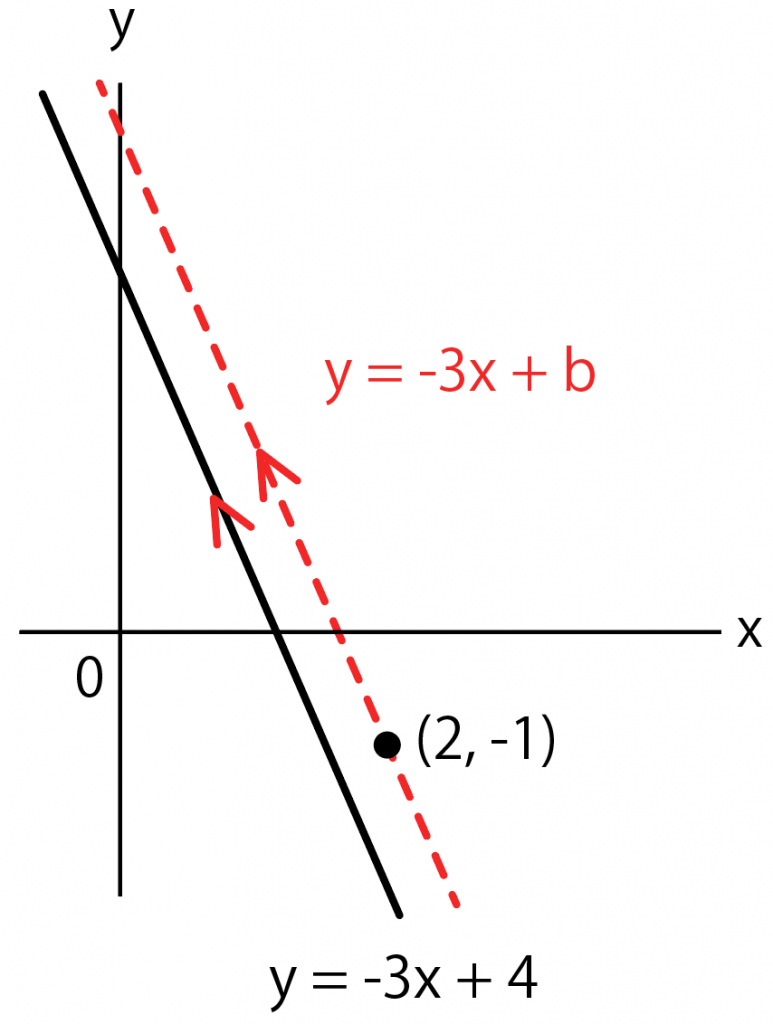
一次関数 テストに出やすい 平行な直線の式の求め方 Qikeru 学びを楽しくわかりやすく

高校2年 数学ii 点と直線の距離 夏季課題 赤城 ᐡᐤᐡ

すど とりあえず 点と直線の距離 の第一歩として原点と直線の距離について このイラストの内容がまず伝わってください 乱暴

直線の式の求め方 思考力を鍛える数学

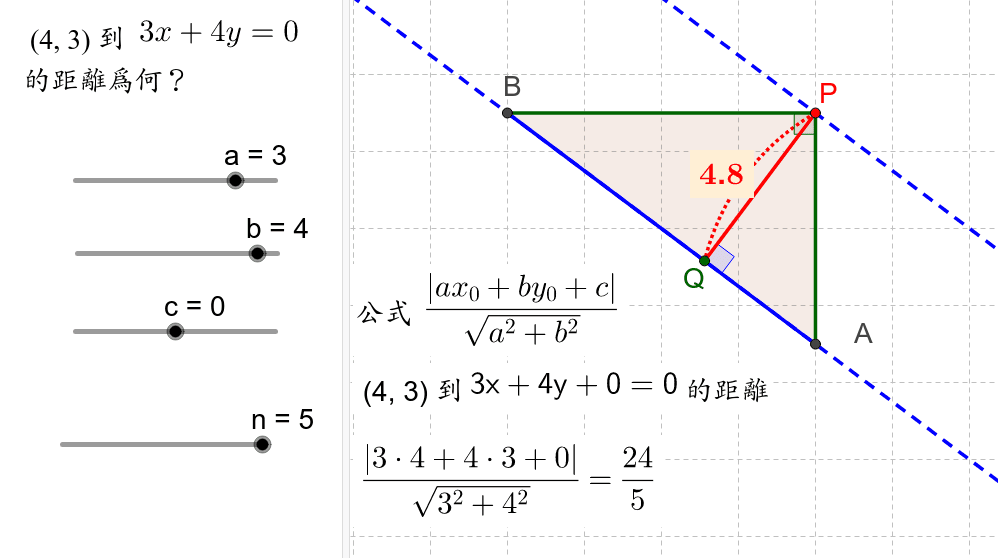
點到直線距離7 距離公式 Geogebra

なぜ 平行な直線の方程式は ０になるのですか Clearnote

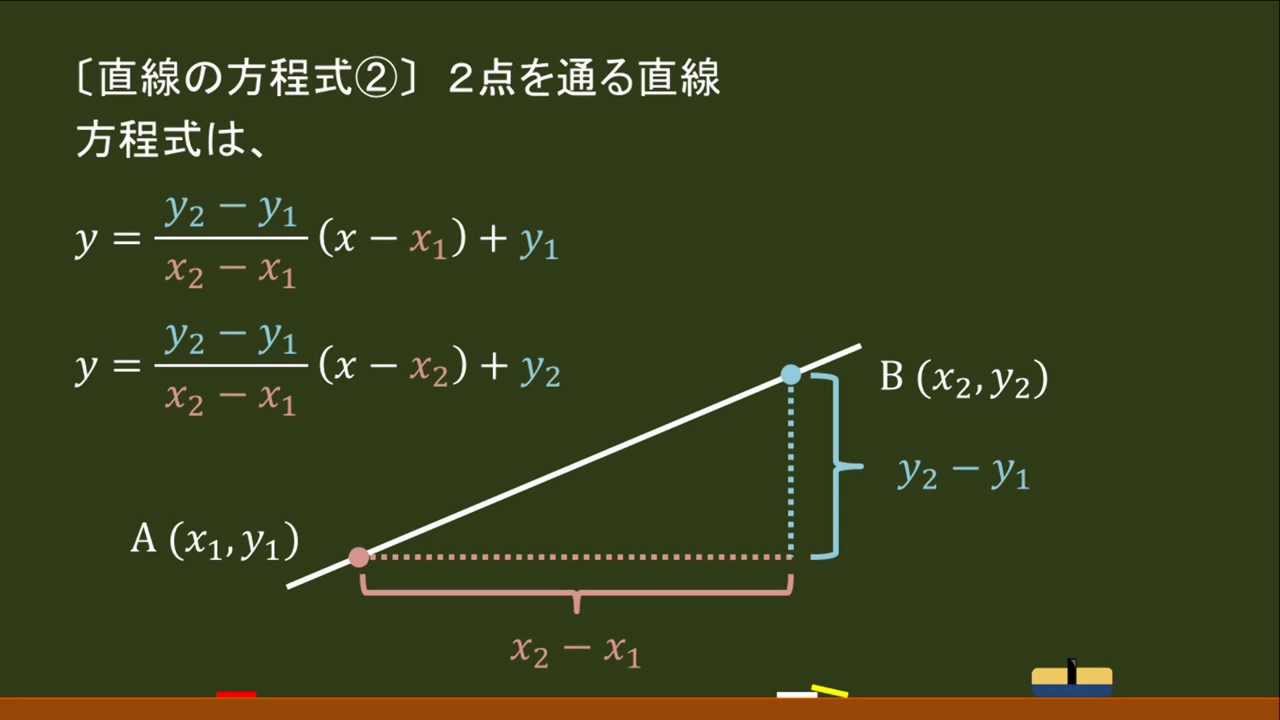
高校数学 直線の方程式の求め方 異なる２点 オンライン無料塾 ターンナップ Youtube

1

ベクトル方程式を超わかりやすく解説した 理系ラボ

1

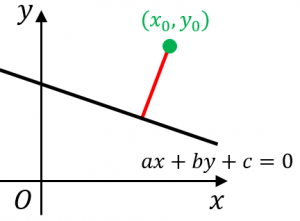
点と直線の距離の公式の意味と中学数学範囲での証明 具体例で学ぶ数学

Incoming Term: 直線の公式, 直線の公式 3次元, 直線の公式 ｙ＝１, 直線の公式 原点 垂線,